2.哥白尼革命

2.5 行星运动定律

1.开普勒行星运动第一定律与行星轨道的形状有关：

行星的轨道是椭圆(而不是圆)，太阳位于椭圆的一个焦点上。

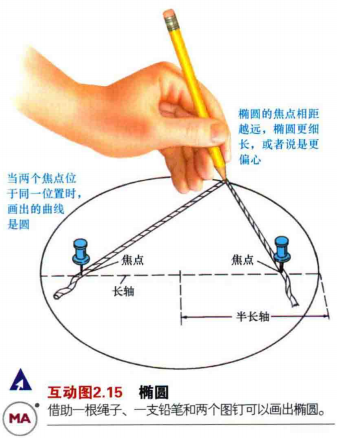
2.椭圆是个扁平的圆。如图2.1说明了如何用一根绳子和两个图钉在构造一个椭圆。图钉固定绳子的每个点被称为椭圆的焦点。包含两个焦点的椭圆上两点的连线被称为长轴。长轴的一半被称为半长轴，用于描绘椭圆的大小。圆是两个焦点恰巧重合的特例；它的半长轴等于圆的半径。

3.椭圆的偏心率用于简单衡量其扁平度。偏心率定义为两个焦点之间的距离与长轴的长度之比。当偏心率等于零时对应于椭圆不椭------完美的圆；而偏心率等于1时，意味着椭圆会被压扁为一条直线。

图2.1

4.开普勒第二定律着眼于星星在轨道不同部分的运动速度：

一条假想的连接太阳和任意行星的连线在相同时间间隔内扫过相同的椭圆面积

5.绕太阳运动时，图中的行星在相同时间段内划出标记分别为A、B和C的弧段。不过请注意，行星沿弧段C运动的距离要比沿弧段A和B运动的距离要长。

6.由于时间相同而距离不同，因此行星的运动速度一定有所不同。当行星靠近太阳时，比如在弧段C处，行星运动比距离太阳远时(如在弧段A处)要快得多。(如图2.2)

图2.2

7.开普勒第三定律增加了关于行星轨道大小与其轨道周期的第三定律：

行星轨道周期的平方正比于它轨道半长轴的立方

8.当我们选择以年作为时间单位、以天文单位作为距离单位时，该定律变得异常简单。一天文单位(AU)等于地球绕日轨道的半长轴------实质上是日地平均距离。

9.我们可以针对任意行星将开普勒第三定律改写为：

$P^2(地球年)=a^3(天文单位)$

10.其中P是行星轨道周期，a是行星轨道半长轴的长度。第三定律意味着行星的轨道周期P增加的比对应的轨道大小a快得多。

11.例如地球轨道半长轴为1AU，轨道周期为1地球年。金星轨道大小约为0.7AU，完成一整圈运动仅需要0.6地球年。

12.表2.1展示了太阳系行星的一些基本量。其要点有：

除水星之外，行星的轨道接近于圆形
行星距离太阳越远，轨道周期接近于圆形
行星距离太阳越远，轨道周期越长

2.6太阳系的规模

1.开普勒定律使我们能够构建一个太阳系的比例模型。虽然所有行星的轨道都有着正确的形状和相对大小，但这并不能告诉我们任何轨道的实际大小。我们可以只用日地距离来表示到每颗行星的距离。

2.20世纪中期之前，最为准确的天文单位的测量是在罕见的水星和金星凌日期间，利用三角测量得到的------也就是这两颗行星正好从太阳和地球之间穿过的短暂时刻。

3.现代，获得太阳系绝对标度，用千米数来表示尺度的大小，而不是只用相对地球轨道的大小的方法是通过雷达。

4.在这种技术中，无线电波被传送向某一天体，比如一颗行星。雷达回音表明了天体的方向和范围，并用绝对单位表示------用千米而不是天文单位表示。

2.7牛顿定律

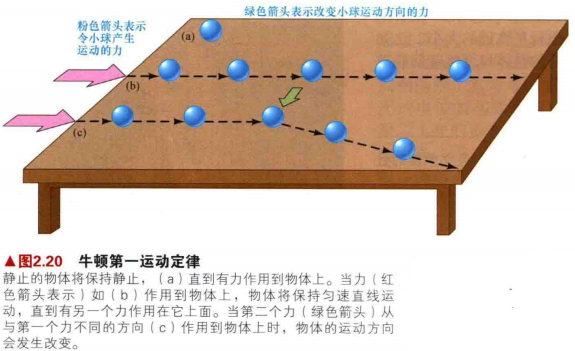
1.如图2.3展示了牛顿第一定律：

每个物体保持静止状态或是匀速直线运动状态，除非它受到外力作用而被迫改变运动状态。

2.第一定律简单说明了运动的物体将沿直线运动，除非有某种外力------推或者拉------改变它的速度或者运动方向。

3.我们大多数人所熟悉的另外一种力的例子是重力------引力将你往地心拖拽时产生的力量。

4.除非受到外力的影响，否则物体保持运动速度和运动方向不变的趋势被称为惯性。牛顿第一定律意味着物体不需要外力来保持匀速直线运动。

5.我们所熟悉的测量物体惯性的量是质量。物体的质量越大，惯性越大，并且需要更大的力才能改变它的运动状态。

6.牛顿第一定律描述的是匀速直线运动------也就是说，运动的速度保持不变。物体的速度包括速度的大小以及速度在空间中的方向。

7.例如石块做匀速圆周运动。石块的速率是常数，但运动方向在变化，因此石块的速度是持续变化的。

图2.3

8.物体速度的变化率------加速、减速或只是改变方向------被称为物体的加速度，这正是牛顿第二定律的主题，他描述为物体的加速度与作用力大小成正比，与物体质量成反比：

当力F作用到质量为m的物体上时，它产生的加速度a等于力除以质量。亦即，a=F/m或F=ma。

9.因此，作用在物体上的力越大或者是物体的质量越小，物体的加速度越大。如果两个物体受到同样大小的力的牵引，质量越大的物体的加速度越小；如果两个相同的物体受到不同大小的力的牵引，受到作用力越大的物体的加速度越大。

10.加速度是速度的变化率，因此它的单位是速度单位除以时间单位，如米每二次方秒(m/s²)。

11.在地球表面，重力使所有物体产生约为9.8m/s²的向下的加速度，而与物体的质量无关。

12.最后，牛顿第三定律简单地告诉我们，作用力不是独立发生的(力的作用是相互的)：

对于每个作用力，都有一个与之相等的，方向相反的反作用力。

13.换句话说，如果物体A在物体B上施加一个力，那么物体B比如也对物体A有大小相等的作用力，但方向相反。

14.只有极端情况下------当速率接近于光速时------牛顿运动定律不再适用。

15.力可能是瞬间的，也可能是持续的。本垒打中，棒球棒施加的力当然能被看成是瞬时的力。力持续施加的例子就是引力。

16.牛顿假设任何有质量的物体都受到其他大质量物体万有引力的吸引。物体质量越大，它的引力就越强。

17.万有引力的大小取决于吸引物体的质量。事实上，力的大小正比于两个物体的质量。

18.行星运动的研究揭示了万有引力的第二面。在距离太阳中心等距离的位置上，万有引力的大小相等，并总是指向太阳。

19.太阳对行星的引力随行星到太阳距离的增加而按平方反比例减小。万有引力因此是服从平方反比定律的。如图2.4所示，这种平方反比力随着距离引力源的增加而迅速减小。

图2.4

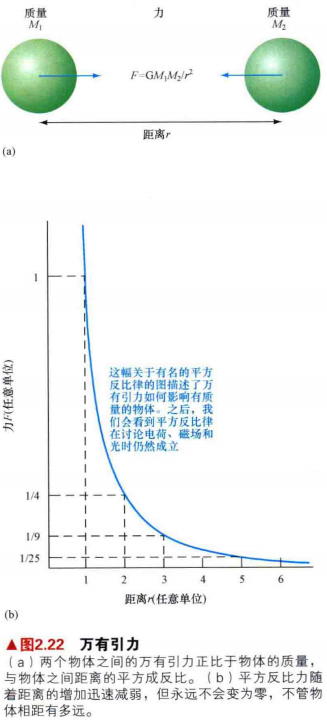
20.我们可以把之前有关质量和距离的描述结合起来，组合任何有重量的物体彼此吸引都服从的引力定律：

宇宙中所有物质粒子彼此之间都相互吸引，力的大小正比于产生作用的粒子的质量，与粒子中心之间相距距离的平方成反比。

按照比例关系，万有引力定律写成：

$引力的大小 \varpropto \frac{物体1的质量\times物体2的质量}{物体之间的距离^2}$

计算距离为r的，两个质量分别是m1和m2的物体之间的引力F的方法通常可以更简洁地表示如下：

$F=\frac{Gm_1m_2}{r^2}$

其中G被称为引力常数，或者通常被简称为牛顿常数，是宇宙的基本常数之一。

$G的数值大小为6.67\times10^{-11}N·m^2/kg^2$

2.8牛顿力学

1.用牛顿万有引力来表述，太阳和行星之间的相互吸引导致了我们所观测到的行星轨道。如图2.5所示，这种引力不断地把每颗行星向太阳牵拉，使行星运动方向发生偏转，变成弯曲的轨道。

2.太阳的质量比任何行星都要大得多，因此它主导了这种相互作用。我们或许可以说是太阳"控制"了行星，而不是相反的情况。

图2.5

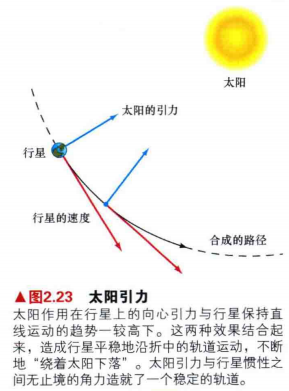
3.在太阳系中，地球正在万有引力和惯性的组合作用下运动。最终造就的是一个稳定的轨道。

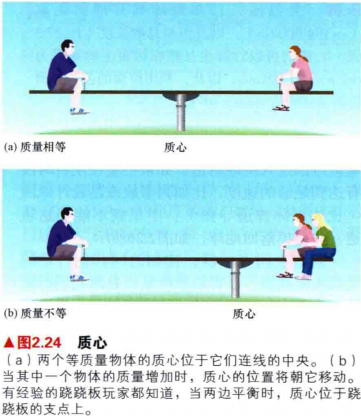
4.事实证明，行星并不是正好以太阳为中心运动的。相反，行星和太阳都绕着它们共同的质心运动------质心是构成两个物体的所有物质的"平均"位置(图2.6所示)。

5.由于太阳和行星受到大小相等、方向相反的引力作用，因此太阳一定也在行星的引力影响下运动。然而，太阳的质量比任何行星的质量都要大得多，因此，行星------太阳构成系统的质心非常靠近太阳的中心，正是开普勒定律如此明确的原因。

6.开普勒第一定律变成：

行星绕太阳运动的轨道是一个椭圆，行星------太阳所构成的系统的质心是椭圆的一个焦点。

图2.6

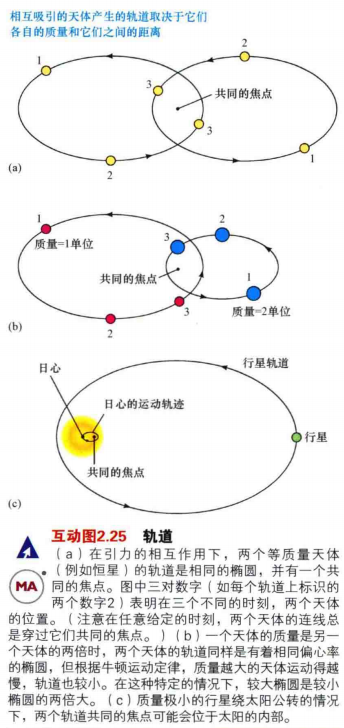
7.如图2.6所示，两个质量类似的物体的质心不会位于任何一个物体内部。若质量相等的物体互相绕转，如图2.7a所示，轨道是两个同样的椭圆，其中一个共同的焦点位于两个物体的中央。

8.对于质量不等的物体，如图2.7b所示，两个椭圆轨道也有一个共同的焦点，并且偏心率相等，但是质量稍大的物体运动得较慢，轨道也更小。

9.对于行星绕太阳公转的情况，开普勒第三定律的修正也不大，但在其他一些情况下却非常重要，例如两颗恒星在彼此引力束缚下的轨道运动。

10.按照牛顿理论，行星相对太阳的轨道半长轴a(以AU为单位)与其轨道周期P(以地球年为单位)的真正关系：

$P^2(地球年)=\frac{a^3(天文单位)}{M_全(以太阳质量为单位)}$

11.其中M全是两个天体质量的总和。注意牛顿对开普勒第三定律的重述保留了轨道周期和半长轴长度的正比例关系，但现在的比例关系包含了质量，因此该关系对所有行星来说并不完全相同。

图2.7

12.给太阳称重。我们假定轨道为圆轨道下，设想一颗质量为m的行星以速度v绕太阳在半径为r的轨道上运动，太阳的质量为M。即使行星运动的速度是常数，但其运动的方向并不是不变的，因此行星速度实际上是变化的------行星在加速。

$\small 行星的加速度为\\ a=\frac{v^2}{r}\\ 因此，根据牛顿第二定律，要使行星保持在轨道上，所需的力是\\ F=ma=\frac{mv^2}{r} 让该方程等于由太阳引起的引力，我们得到\\ \frac{mv^2}{r}=\frac{GmM}{r^2}\\ 因此行星在圆轨道上的速度为\\ v=\sqrt{\frac{GM}{r}}$

13.由于我们测量得到了G，我们知道一年的长度和天文单位的大小，因此我们可以带入常量。

$已知量v=30km/s(由椭圆周长和时间算出),r=1AU=1.5\times10^{11}m,以及G=6.7\times10^{-11}{Nm}^2/{kg}^2,我们计算得到太阳质量为：\\ 2.0\times10^{30}g$

14.某些空间飞行器，获得的速度足以逃离我们行星的引力并永远离开地球。该速度被称为逃逸速度。

15.然而，当速度比逃逸速度大时，宇宙飞船将永远地飞离地球。行星、恒星、星系------所有有引力的天体------都有逃逸速度。

16.不管天体的质量有多大，引力都会随着距离的增大而减小。于是，逃逸速度也就随着距离的增加而减小。我们距离地球越远，就越容易逃离引力的束缚。

17.如果一个天体的运行速度大于逃逸速度，那么它的运动可以说是开放的，轨道也不再是椭圆。事实上，这时宇宙飞船相对于地球的运动轨迹在几何上被称为双曲线。