6.恒星

6.1太阳邻近区域

1.视差是随着观测者视线的变化，前景物体相对于遥远背景的视位移。

2.如图6.1所示，在一年中不同的时刻观测同一颗恒星，然后再比较我们的观测，我们可以将基线延长为地球绕太阳公转轨道的直径，即2AU。

3.只有利用这样非常长的基线，某些恒星的视差才是可测量的。随着我们从地球公转轨道的一端运动到另一端，恒星的视差角------通常被定义为它相对于背景的视位移的一半。

4.由于恒星视差如此之小，天文学家发现用角秒来度量视差比用角度方便。

5.1秒差距(1pc)，即"一角秒的视差"，指的是一颗观测到的视差正好等于1"的恒星的距离。

$1pc=206265AU=3.1\times10^{16}m$

6.由于视差随着距离的增加而减小，我们可以用以下公式来讲恒星的视差和距离联系起来：

$距离(以秒差距为单位)=\frac{1}{视差(以角秒为单位)}$

7.因此，测量视差为1"的恒星距离太阳为1pc。秒差距的定义使得距离和视差角之间的转换变得容易：一个视差为0.5"的天体距离为2pc，一个视差为0.1"的天体距离为10pc，以此类推。1pc大约等于3.3光年。

图6.1

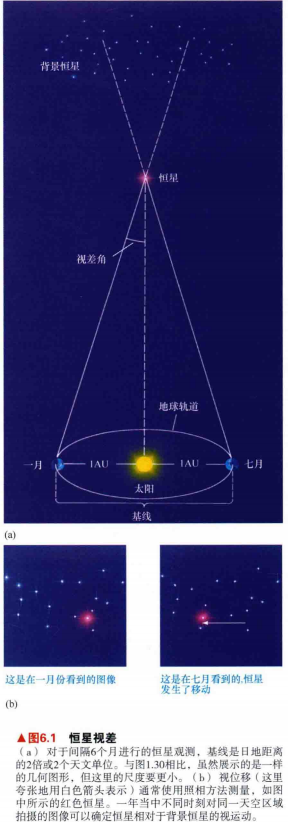
8.距离地球(即太阳)最近的恒星是半人马座的比邻星。这个恒星是一个三聚星系统的成员之一(三颗独立的恒星彼此互相绕转，并由引力束缚在一起)。比邻星的视差为0.77"，这意味着它的距离约为1.3pc(4.3光年)。最近的恒星到地球的距离差不多是日地距离的300000倍！在银河系内，这是一个相当典型的恒星际间的距离。

9.视差除了造成恒星的视运动外，恒星本身在星系间也有空间运动。

10.恒星运动包括两部分：

恒星的视向速度------沿着视线方向的速度，可以用多普勒效应来测量。
恒星的横向速度------垂直于视线方向的速度，可以通过仔细地监测恒星在天空中的运动来确定。

11.从地球上观测并修正视差后得到地恒星在天空中的周年运动被称为自行。它描述了恒星相对于太阳的运动速度的横向分量(在银河系内运动时，恒星和太阳都有空间运动；然而，从地球上观测，只有他们之间的相对运动会改变恒星在天空中的位置)和视差一样，自行的测量也以角位移表示。

12.虽然恒星的横向速度一般非常大------几十甚至几百千米每秒------但它们距离太阳都很遥远，意味着它们的自行会很小，通常我们需要花很多年才能觉察出它们在天空中的运动。

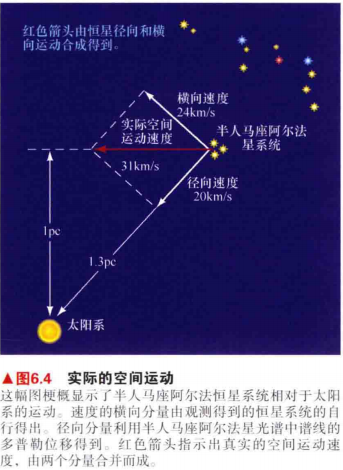
13.如图6.2展示的是实际的空间运动。测量到半人马座阿尔法星1.35pc的距离处，这一测量结果意味着横向速度为24km/s。我们可以利用多普勒效应来确定另一运动分量------视向速度。计算过程：

$\small \begin{aligned} &半人马座阿尔法星的谱线稍微蓝移了约0.0067\%，可以测得该恒星系统的视向速度为300000km/s\times6.7\times10^{-5}=20km/s。 \end{aligned}$

图6.2

6.2光度和视亮度

1.光度是恒星的固有属性------它完全不依赖于观测者的观测位置和运动速度。

2.当我们观测一颗恒星时，我们所见的并不是恒星的光度，而是它的视亮度------在单位时间内到达单位面积的某种光敏表面或装置(比如电荷耦合器件(CCD)芯片或人眼)的总能量。

3.视亮度测量的不是恒星的光度，而是从地球上观测时所接收到的来自于恒星的能量通量。一颗恒星的视亮度，取决于其距地球的距离。

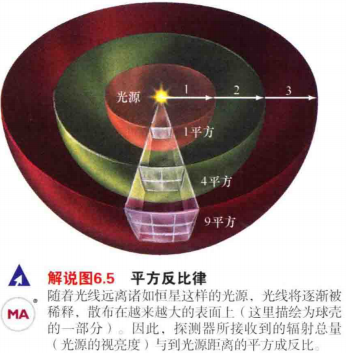
4.图6.3展示了光线如何离开恒星并在太空中传播。辐射向外移动，穿过以光源为中心的半径不断增加的假想球体。单位时间内离开恒星的辐射总量------恒星的光度是常数，因此光线传播的距离光源越远，穿过每单位面积的能量越少。

5.随着能量扩散到太空中，能量传播的面积越来越大，因此能量更加分散。

6.由于球体的面积随着半径的平方增长，因此单位面积内的能量与到恒星距离的平方成反比。

图6.3

7.恒星的光度也会影响它的视亮度。当距离相同时，视亮度与光度呈线性关系。所以恒星的视亮度与恒星的光度成正比，与距离的平方成反比：

$视亮度(能量通量)\varpropto \frac{光度}{距离^2}$

8.两颗不一样的恒星也可能有着同样的视亮度，没有额外信息的话，我们无法分辨光度增加和距离减少所带来的影响。

9.天文学家通常使用星等标度的概念来测量视亮度。

10.现代天文学家使用的星等标度方法概述如下。首先，我们定义天体5个星等的变化对应于视亮度恰好变化100倍。第二，由于我们讨论的是视亮度，因此依巴谷分级系统中的数字被称为视星等。第三，标度不再局限为整数；视星等为4.5等的恒星视亮度介于4等星河5等星之间。最后，星等扩展到1等和6等之外。

11.当把恒星放在距离观测者10pc时，所得到的恒星视星等被称为其绝对星等。由于在这样的定义下，恒星的距离固定，因此绝对星等测量的是恒星的绝对亮度，即光度。

12.依巴谷定义的1至6等的范围所覆盖的视亮度变化约为100倍——1等星比6等星要亮100倍。其次，人眼的生理特点决定了，星等没变化1等，对应的视亮度变化约为2.5倍。

补充知识------星等标度的更多知识

1.绝对星等相当于恒星的光度------恒星的内禀属性。

2.给定太阳的绝对星等是4.83以后，我们可以根据这两个量建立一个转换图(如图6.4)。由于亮度增加100倍对应于星等减少5个单位，那么光度是太阳光度100倍的恒星的绝对星等为4.83-5=-0.17，而光度为0.01太阳光度的恒星的绝对星等为4.83+5=9.83。

图6.4

3.示例一：

$\small \begin{aligned} &让我们计算绝对星等为\bm{M}(绝对星等的惯用符号，不要与质量混淆)的恒星的光度(以太阳光度为单位)。\\ &这颗恒星的绝对星等与太阳的绝对星等相差(\bm{M}-4.38)等。\\ &因此根据刚才的推导关系，恒星光度L与太阳光度的差别为100^{-\frac{\bm{M}-4.83}{5} }，即10^{-\frac{\bm{M}-4.83}{2.5} }。\\&因此我们可以写成:\\ \end{aligned}\\ \small \bm{L}(太阳光度)=10^{-\frac{\bm{M}-4.83}{2.5} }$

4.示例二：将平方反比律加到这些公式中，恒星的距离增加10倍，它的视亮度会降低100倍，因此它的视星等增加5等；距离增加100倍，视星等增加10等，以此类推。距离每增加10倍，视星等都会增大5等。由于绝对星等无非是距离为10pc的视星等，因此我们可以写为：

$视星等-绝对星等=5\log_{10}{\frac{距离}{10秒差距}}$

6.3恒星温度

1.如图6.5，较冷的红色恒星参宿四和较热的蓝色恒星参宿七的颜色清晰可见。这些颜色是恒星的内禀属性，与多普勒红移和蓝移毫不相关。如果我们要得到这些恒星的温度，需要依靠辐射定律和恒星光谱的详细性质。

图6.5

2.天文学家可以通过测量恒星在某些频率的视亮度(能量通量)，然后将这些观测与适当的黑体曲线进行匹配，从而确定恒星的表面温度。

3.由于我们对黑体曲线的基本形状了解充分，因此天文学家可以仅仅利用两个波长处的观测来估计恒星的温度。这一目标可以通过使用望远镜滤光片来屏蔽特定波长范围之外的所有辐射来达到。

4.如图6.6所示，B和V滤光片准许不同温度的天体辐射透过的光量不同。曲线(a)对应于非常炽热的，温度为30000K的辐射源，透过B滤光片的辐射比透过V滤光片的辐射要多得多，因此该天体在B滤光片中看起来要比V滤光片亮。

5.曲线(b)对应的温度为10000K，通过B和V滤光片的流量大致相等。曲线©对应的温度为3000K，V滤光片范围内接收到的能量比B滤光片得到的图像比V滤光片得到的图像弱得多。

图6.6

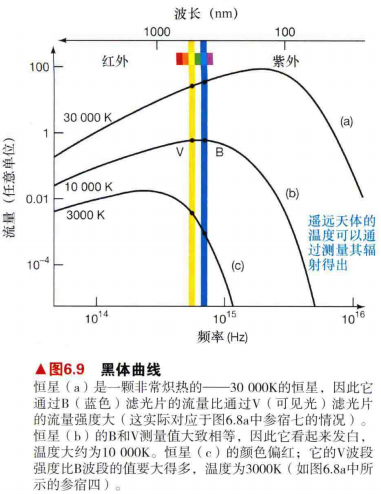
6.天文学家可以简单地通过测量和比较透过不同颜色的滤光片所接收到的光来估计恒星的温度。

7.测光是指利用标准的滤光片组进行的非谱线分析。

8.表6.1列出了使用测光方法得出的几颗著名的亮星的表面温度，以及设有滤光片时恒星呈现出的颜色。

表6.1

表面温度/K	颜色	例子
30000	蓝-紫	参宿三
20000	蓝	参宿七
10000	白	织女星，天狼星
7000	黄-白	老人星
6000	黄	太阳，南门二
4000	橙	大角星，毕宿五
3000	红	参宿四，巴纳德星

9.颜色是对恒星有效的描述方式，但天文学家常常会结合从光谱观测中获得的额外恒星物理信息，使用一种更加复杂的策略来对恒星属性进行分类。

10.如图6.7显示了一些恒星在长波范围内有很强的吸收线。其他恒星在短波范围内有很强的吸收线。还有一些恒星的强吸收线覆盖了整个可见光谱的范围。

11.尽管许多元素的谱线展示出广泛的强度变化，但图6.6中光谱的区别并不在于成分的不同。

图6.7

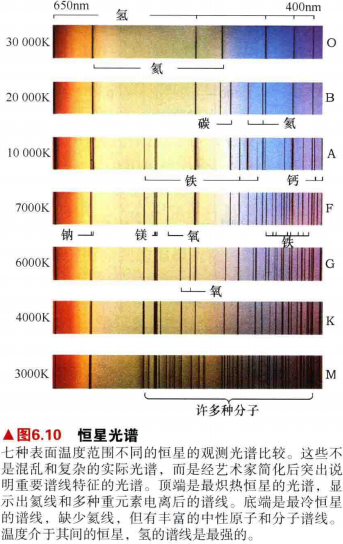
12.详细的谱线分析表明这七颗恒星有着类似的元素丰度------都与太阳丰度大致相当。谱线差异几乎完全来自于恒星的温度。

13.图6.7中光谱的主要区别在于：

表明温度超过25000K的恒星光谱通常有着一次电离氢(氢原子失去一个轨道电子)和多次电离的重元素的强吸收线，如氧，氖和硅。较冷恒星的光谱中没有这些强吸收线，是因为只有非常炽热的恒星才能激发和电离这些紧密束缚的原子。
相比之下，在非常炽热的恒星的光谱中，氢的吸收线相对较弱。原因并不是因为缺乏氢，氢是迄今为止所有恒星中最为丰富的元素。然而，在高温下，多数氢被电离，因此很少有完整的氢原子来产生强烈的谱线。
表面温度居中的、大约为10000K的恒星中氢的谱线最强。这一温度正好适合电子频繁地在氢的第二和更高轨道之间运动，从而产生特有的可见氢谱线。束缚紧密的原子的谱线需要大量的能量才能被激发出来，因此在这些恒星的光谱中很少被观测到，而束缚较为松散的原子的谱线在这些恒星的光谱中出现得相当普遍。

14.决定一颗恒星光谱外观得主要因素是它得温度，恒星光谱是测量这些重要恒星性质得强大、精确得工具。

15.最炽热得恒星用O表示，因为他们的氢吸收线非常弱，在原来的策略下被分类到最后。按照温度降低的顺序，现在保留下的字母为O、B、A、F、G、K、M。这些恒星类型被称为光谱型。记忆方法：“Oh,
Be A Fine Girl, Kiss Me”。

16.天文学家进一步将每个字母光谱类型细分为10个子类，用数字0~9表示。按照惯例，数字越小，恒星越炽热。

17.附表6.2恒星光谱型：

表6.2

光谱型	表面温度/K	显著吸收线	常见例子
O	30000	强电离氦线；重元素的多次电离谱线；弱氢谱线	参宿三(O9)
B	20000	中等强度的中性氦线；重元素的一次电离谱线；中等强度的氢线	参宿七(B8)
A	10000	非常弱的中性氦线；重元素的一次电离谱线；强氢线	织女星(A0),天狼星(A1)
F	7000	重元素的一次电离谱线；中性金属谱线；中等强度氢线	老人星(F0)
G	6000	重元素的一次电离谱线；中性金属谱线；相对较弱的氢线	太阳(G2),半人马座阿尔法星(G2)
K	4000	重元素的一次电离谱线；强中性金属线；弱氢线	大角星(K2),毕宿五(K5)
M	3000	强中性原子谱线；中等强度的分子谱线；非常弱的氢线	参宿四(M2),巴纳德星(M5)

6.4恒星的大小

1.有些恒星足够大、足够亮，距离也足够近，使得我们能够直接测量它们的大小。著名的例子就是参宿四，它几乎大到短波上能够被哈勃太空望远镜分辨出来。

2.一旦能够测量恒星的角大小，如果它的距离也已知，那么我们就可以利用简单的几何方法确定它的半径。由于恒星存在变星(我们通常讨论最大半径，因为变星的半径和光度有着不太规则的变化)。

3.大多数恒星的距离都太遥远或是太小，而无法采用这样的直接测量方法。相反，它们的大小必须通过间接方法------利用辐射定律推断出来。

4.恒星发出的辐射由斯特藩-玻尔兹曼定律决定，即恒星表明单位面积在单位时间内辐射的能量与恒星表明温度的四次方成正比。

5.为了确定恒星的光度，我们必须乘以它的表面积------同一温度下，个头大的天体所辐射的能量比个头小的天体所辐射的能量多。由于表面积正比于半径的平方，于是有：

$光度\propto半径^2\times温度^4$

这一半径-光度-温度关系很重要，因为它表明已知恒星的光度和温度，如此便可推导并估计恒星的半径。

补充知识------估计恒星的半径

1.我们可以结合斯特藩-玻尔兹曼定律和球体面积公式，从而得到正文中所描述的半径-光度-温度关系：

$\small 光度(L)、半径(R)和温度(T)之间的关系：\\ \begin{cases} &L=AF&(1)\\ &A=4{\pi}R^2&(2)\\ &F={\sigma}T^4&(3) \end{cases}\\ 由1,2,3得L=4{\pi}{\sigma}R^2T^4$

2.如果我们使用"太阳"得单位，我们可以将公式改写成：

$R^2(太阳半径)\times{T^4}(以580为单位)$

为了利用恒星得光度和温度来计算恒星得半径，我们重新改写公式如下:

$R=\frac{\sqrt{L}}{T^2}$

6.巨星是半径为10~100倍太阳半径的恒星。由于4000K的天体颜色看起来偏红，因此毕宿五是一颗红巨星。更大的，半径超过1000个太阳半径的恒星被称为超巨星。参宿四就是红超巨星的一个典型例子。

7.矮星指的是一切半径与太阳或者更小的恒星(包括太阳自身)。由于8500K的天体看起来发白------因此炽热的南河三是白矮星的一个例子。

6.5赫罗图

1.天文学家使用光度和表面温度来进行恒星分类。

2.如图6.8给出了几颗著名恒星的光度与温度关系图。这种形式的图被称为赫茨普龙-罗素图，简称赫罗图。

$\small 该图纵坐标以太阳光度为单位表示(3.9\times{10^{26}}W),覆盖了很大的范围，从10^{-4}到10^4;太阳正好出现在光度范围的中间位置，光度为1。\\ 横坐标表示的是表面温度，和传统的温度从左到右增加的表示方法不同，温度从\textbf{\textcolor{red}{右到左}}是增加。$

图6.8

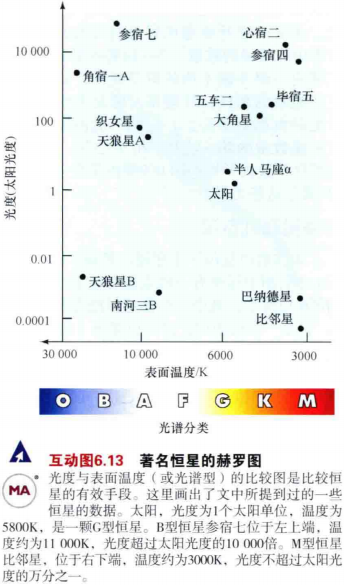
3.天文学家常常使用恒星的颜色来表示它的温度。但事实上，图6.8中沿着水平轴画出的光谱型相当于B/V颜色指数。另外，由于天文学家通常用绝对星等来表示恒星的光度，因此也可以作为此图的纵坐标轴。许多天文学家更愿意将他们的数据用这样更有"观测性"的方式来表示，这是对应于图6.8被称为颜色-星等图。

4.随着赫罗图绘制的恒星数目增多，存在一种关系：恒星并不是均匀分布在赫罗图上的；相反，大部分恒星被限制在一个相当明确的带状区域内，从左上顶端(高温、高光度区)沿对角伸展到右下底部（低温、低光度区）。换句话说，温度低的恒星往往较暗（低光度），而炽热的恒星往往比较明亮（光度更高）。这样一条跨越赫罗图的横向带被称为主序。

5.如图6.9包含约80颗距离太阳在5pc以内的恒星，显示出对恒星性质更为系统的研究。随着图中包含的点越来越多，主序逐渐被"填满"，主序的图像变得更加清晰。绝大多数太阳邻近区域内的恒星都位于主序位置。

6.主序星的表面温度范围从3000K左右到30000K以上。这样相对较小的温度范围主要是由恒星内核发生的核反应速率所决定的。

7.利用半径-光度-温度关系，天文学家发现，恒星半径也沿主序在变化。赫罗图右边地段的暗弱红色M型恒星大约只有太阳半径的十分之一大，而左边顶部明亮的蓝色O型恒星大约比太阳大10倍。

图6.9

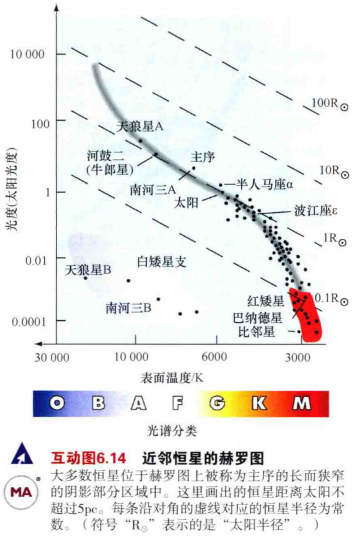
8.沿着主序从上到下，我们能发现一个非常清晰的变化趋势。左上端，恒星很大、很热、很亮。鉴于它们的大小和颜色，它们被称为蓝巨星。最大的是蓝超巨星。在右下端，恒星很小、很冷、很暗，它们被称为红矮星。红矮星是天空中最为常见的恒星。

9.如图6.10所示。更多光度极大的恒星位于主序的上端，而不是下端。图中蓝巨星更多的原因是：我们在很远的距离上只能看见光度非常大的恒星。这幅图显示的恒星散布的空间范围比图6.9中显示的那些恒星要宽广得多，但它们几乎都偏向光度较大的那边。

10.事实上，天空中最亮的20颗恒星中，只有6颗距离我们10pc内；尽管剩下的恒星很遥远，但由于它们的光度很大，因此也能被看到。

图6.10

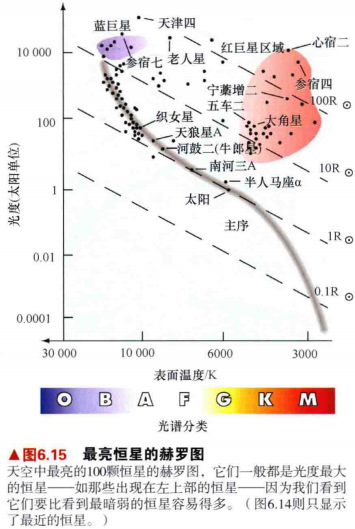
11.大多数恒星位于主序段。但是如图6.9。位于赫罗图的左下角，存在更多如南河三这样暗弱但炽热的恒星。这一区域被称为白矮星支。

12.如图6.8中也显示了毕宿五，它的表面温度为4000K，但光度为太阳光度的300倍左右。这类恒星位于赫罗图的右上角(图6.10)，该区域被称为红巨星支。太阳附近的5pc内没有发现任何红巨星，但天空中可见的许多最亮的恒星实际上是红巨星。

13.尽管红巨星的数量相当稀少，但红巨星却非常明亮，在很远的距离外也能被看见。

14.太阳附近的恒星大约有90%是主序星。

6.6延伸到宇宙距离尺度

1.测量一个光源的视亮度，并结合它本身光度的相关信息，可以用于估计光源的距离。

2.利用恒星的光谱型来推断距离的过程被称为分光视差法。关键步骤：

我们测量恒星的视亮度和光谱型，并不需要知道它的距离有多远。
然后我们利用光谱型来估计恒星的光度。
最后，我们应用平方反比律来确定恒星的距离。

3.主序的存在使得我们能把容易测量的量(光谱型)和恒星的光度联系起来，而光度可能是未知的。术语分光视差指的是利用恒星光谱型来推断光度并由此得到距离的特殊过程。

4.宇宙距离阶梯的第二级------恒星视差------它以第一级阶梯的雷达测量为基础，因为它以地球轨道为基线。我们已经利用前两级阶梯确定了许多近邻恒星的距离和其他物理性质，现在我们可以使用这些知识来构建阶梯的第三级------分光视差。

5.如图6.11展示了恒星的距离对应的宇宙距离阶梯示意图。

图6.11

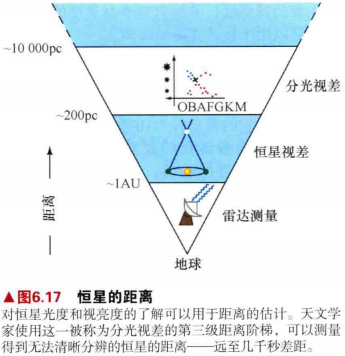
6.分光视差可以用于确定几千秒差距之外的恒星距离。在此距离之外，很难得到单颗恒星的光谱和颜色。"标准"的主序可以利用(几何)视差得到，因此可以利用近邻恒星来对分光视差方法做定标。

7.注意，在使用这种方法时，我们假定遥远恒星从根本上类似于近邻恒星，它们所处的主序同近邻恒星的主序一样。

8.赫罗图中的主序并不是一条线，它有宽度。因此，采用赫罗图得到的光度有着相当大的不确定性，因此得出的恒星距离也有相当大的不确定性。利用分光视差得到的距离，通常精度大约不超过25%。

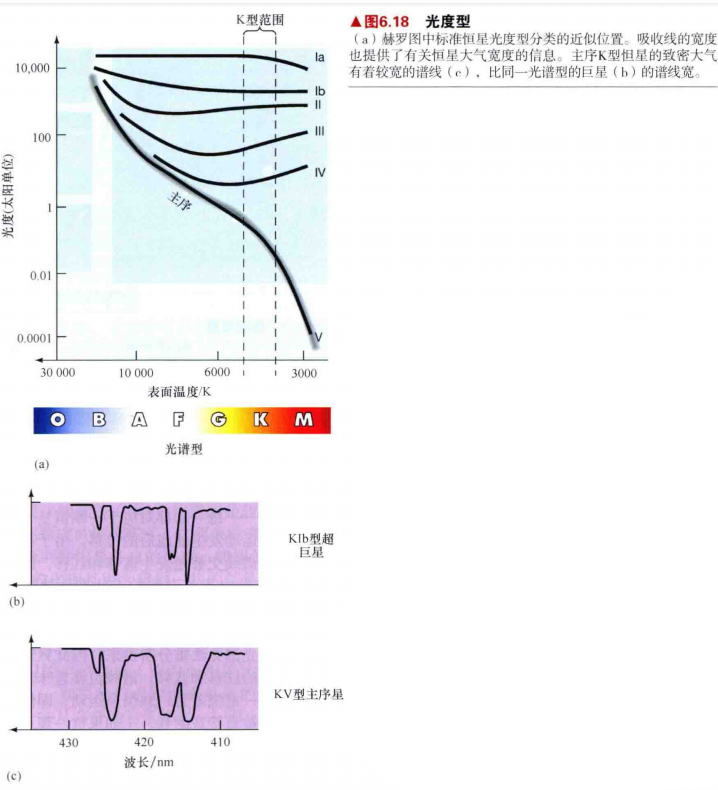
9.如果正在研究的恒星不在主序内，我们需要分析谱线形成处的气体密度信息。红巨星的大气比主序星的大气要稀薄得多，而主序星的大气要比白矮星的大气稀薄得多。

10.由于谱线宽度取决于恒星大气的密度，而密度又与光度密切相关，因此这一恒星属性被称为光度型。标准分类表如表6.3所示，并展示在图6.12a的赫罗图中。

11.通过确定恒星地光度型，天文学家通常可以非常确定地判断该天体属于哪一类。

12.根据完全通过光谱方法测量得到的恒星属性，我们现在可以有办法具体说明恒星在赫罗图中的位置，就像温度和光度那样，光谱型和光度型也将恒星限定在赫罗图的确定位置上。

表6.3恒星光度型

图6.12

6.7恒星质量

1.恒星的质量及其成分最终确定了恒星在主序上的位置。质量和成分是任一恒星的基本属性。它们一起唯一地确定了恒星的内部结构、恒星的外貌，甚至是恒星未来的演化。

2.大部分恒星是两颗或两颗以上的恒星互相绕转组成的多星系统的成员。多数恒星是双星系统，由两颗绕其共同质心运行的恒星构成，在它们相互的引力吸引下聚在一起。

3.天文学家根据从地球上看到的双星外貌和观测它们的难易程度，对双星系统进行了分类。

目视双星的成员间隔较远，足够明亮，可以单独地进行观测和监控(通过天文望远镜观测到)，如图6.13所示
分光双星是指的只有通过分析光谱变化才能辨别的双星。
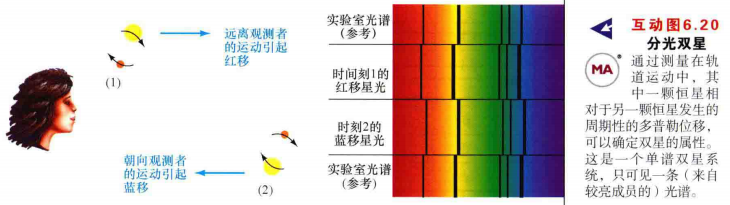
- 最常见的是光谱分光双星，它们的距离很遥远，无法单独分辨它们的成员星，但在监测它们互相绕转时，谱线的前后多普勒位移能够间接地探测它们。朝向观测者的运动会使谱线向电磁波谱的蓝端移动，而远离观测者的运动则会使谱线往红端移动
- 在双谱分光双星中，可见两套有区分的谱线------每一套都对应一颗恒星------随着恒星的运动发生前或后的位移。由于我们发现了特定谱线交替地发生蓝移和红移，因此我们能知道发出这些谱线的天体在绕轨道运行。
- 在更常见的单谱分光双星系统中，如图6.14所示的那些，其中一颗恒星太过暗弱，以至于它的光谱无法被分辨出来，因此只观测到一套谱线的红移或蓝移。谱线位移意味着观测到的恒星一定绕着另一颗恒星运动，即使这颗伴星无法被直接观测到。
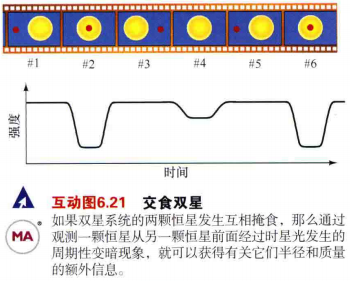
更为少见的是交食双星，这对恒星的轨道平面几乎与我们的视线相平行。在这种情况下，如图6.15所示，随着一颗恒星从另一颗恒星前面通过(掠过)，我们会观测到星光的周期性变暗。通过研究来自于双星系统的光变曲线，天文学家可以详细地推断有关恒星轨道和质量的信息，以及推断出它们的半径。

图6.13

图6.14

图6.15

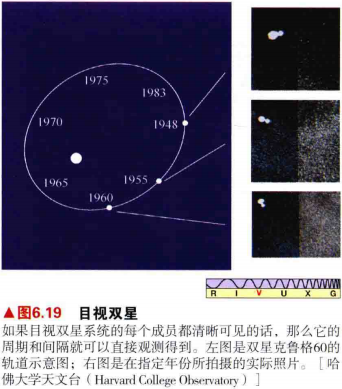
4.目视双星的距离已知，那么可以直接利用简单的几何来确定轨道的半长轴。利用修改后的开普勒第三定律确定双星成员的总质量，那么双星的周期和轨道半长轴的大小就正是我们所必需的条件。之后测量目视双星系统中每颗恒星到质心的距离，可以得到恒星的质量比。知道了总质量和它们的比例，我们就能知道每颗恒星的质量。

5.对分光双星来说，是不可能直接确定它们的半长轴的。多普勒位移测量可以告诉我们有关两颗恒星轨道速度的信息，但只是有关视向速度分量(沿着视线方向的速度)的信息。因此，我们无法确定轨道相对于我们视线方向的倾角，我们无法分辨是一颗轨道侧向我们的、运动缓慢的双星，还是一颗轨道几乎面向我们的、运动快速的双星。

6.对双谱分光双星来说，可以测得各自的视向速度，因此能够确定成员的质量比，但轨道倾角的不确定性意味着只能获得成员个体质量的下限。

7.对单谱分光双星来说，可供使用的信息更少，只能推导出成员质量之间相当复杂的关系(质量函数)。

8.如果一颗光谱双星正好也是一个交食系统，那么轨道倾角的不确定性就没有了，由此可知双星轨道是平着侧向我们。在这种情况下，双谱分光双星两个成员的质量能够被确定。单谱分光双星，如果较亮的那颗恒星的质量能够利用其他手段确定，那么质量函数也可以得以简化，从而知道不可见的恒星质量。

6.8质量和其他恒星属性

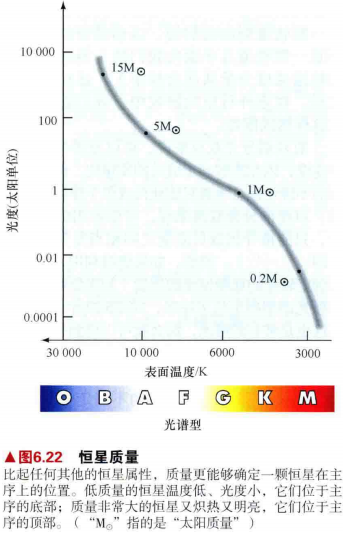
1.如图6.16是一幅简略的赫罗图，说明了恒星质量如何沿着主序变化。从低质量的红矮星到大质量的蓝巨星，都有着明确的连续性。除了少数例外，主序星的质量范围从太阳质量的10%到20倍太阳质量。

图6.16

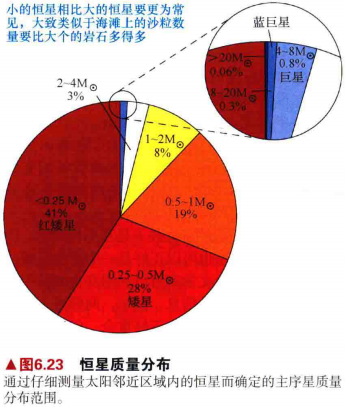
2.图6.17说明了主序星的质量大小是如何分布的。低质量恒星的占比非常高，而质量为几倍太阳质量的恒星的占比非常微小。

图6.17

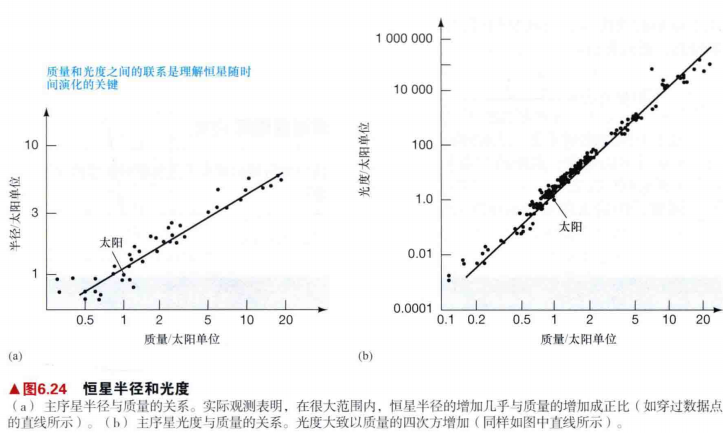
3.图6.18说明了主序星的半径和光度与其质量的关系。基于观测到的双星系统，两幅子图分别显示了质量-半径和质量-光度的关系。

4.沿着主序，恒星半径和光度都随着质量增加。恒星半径的增加正比于恒星的质量，而光度的增加要快得多------差不多是质量得四次方。

图6.18

5.不同恒星之间，中心温度的差别相对较小，而光度的变化很大。恒星内部快速的核燃烧在单位时间内释放了巨大的能量。

我们可以通过下面推理量化恒星寿命和恒星质量、恒星光度的关系。

$恒星寿命\propto\frac{恒星质量}{恒星光度}$

质光关系告诉我们，恒星的光度近似正比于质量的四次方，因此我们可以修改上面的公式，近似得到：

$恒星寿命\propto\frac{1}{恒星光度^3}$

6.例如，O型和B型主序恒星由于内部核反应非常迅速，因此它的燃料很快就被耗尽，尽管它的质量很大。所以，我们观测到的O型和B型恒星都非常年轻。较冷的K型和M型恒星质量比太阳小得多。它们的核心密度和温度都较低，质子反应慢，比太阳核心的反应缓慢很多。单位时间内释放的能量少，使得它们的光度也低。因此它们的寿命非常长。