今日天文恒星从诞生到死亡第一章读书笔记(一)
1.天图量绘 天文学基础
1.1,1.2我们在天空中的位置,科学理论和科学方法
1.宇宙是所有空间,时间,物质和能量的总体,而天文学是研究宇宙的学科。
2.现代科学理论的几个重要特征:
-
理论必须是可测试的
-
理论一定要不断地被测试
-
理论应该是简单的
1.3~1.5 "显而易见"的风景,地球的轨道运动,月球的运动
1.我们把从正午到下一个正午之间的时间间隔(24h)成为太阳日。太阳和其他恒星每天在天空中的运动被称为周日运动。
2.恒星日是地球真实的自转周期——我们的行星自转回到空间中相对于遥远恒星的同一方向所花费的时间。
3.恒星日和太阳日的差异如图
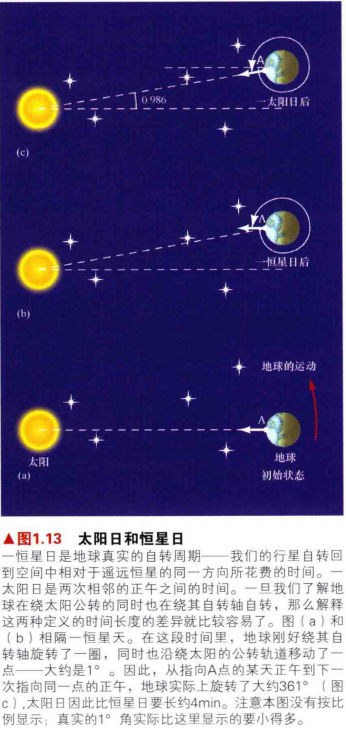
由于地球同时以两种方式运动——地球绕其中心轴自转的同时还绕着太阳公转。每当地球绕其自转轴旋转一周时,它也沿着围绕太阳的轨道移动了一小段的距离。因此地球需要旋转比360°稍微多一点。才能让太阳回到天空中的同一视位置。
补充知识——角度测量
1.完整的圆有360°,每1°的变化可以再进一步细分为度的分数。称为角分——记为’。1°包括60角分,即1°=60’。
2.一个角分也能被分为60个角秒——记为“。1‘包括60角分,即1’=60”。
3.角大小本身并不足以确定一个物体的实际直径——除非物体的距离也已知。
4.天球:是假想出的一个与地球同球心,并有相同的自转轴,半径无限大的球。天空中所有的物体都可以当成投影在天球上的物体。
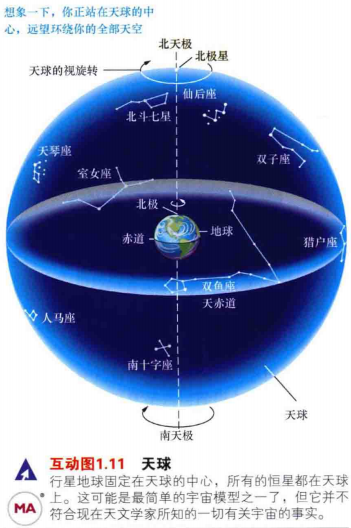
5.地球自转轴和天球的交点被称为天极。北天极正好位于地球北极的正上方。延长地球自转轴到相反方向便是南天极。介于北,南天极正中的是天赤道,代表的是地球赤道平面和天球的交线。
6.黄道:太阳在一年中沿天球运动的视路径被叫做黄道。
7.黄道面是地球公转轨道平面。黄道的倾斜是因地球自转轴与其公转轨道之间存在夹角(23.5°)而造成的。
8.黄道与天赤道的两个交点——当地球自转轴垂直于日地连线时的位置被称为二分点。
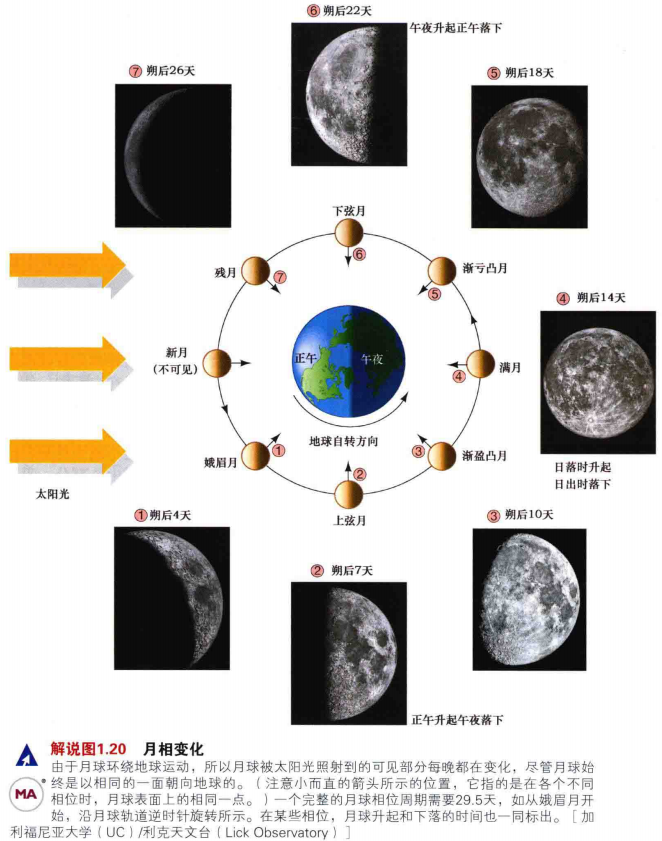
9.月球的外观成为月相。
月相具有规律的周期性变化,需要约29.5天完成一次循环。
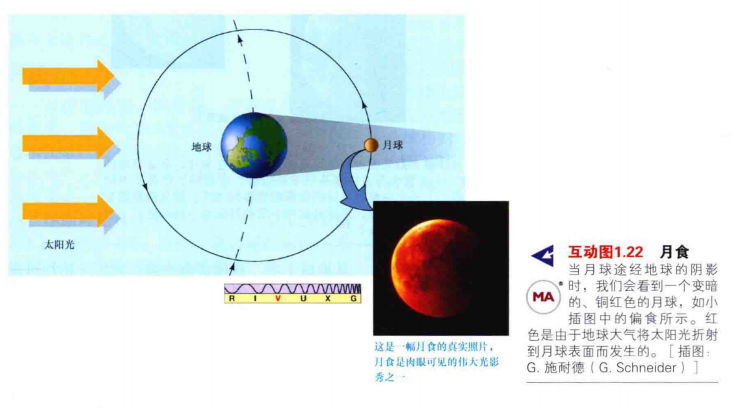
10.有时但仅在朔(新月)或者望(满月)时从地球上看,太阳和月球恰好连成一线,此时我们将观测到被成为”月食“的壮观天象。
11.当从地球来看,太阳和月球刚好处于相对的位置时,地球的阴影会扫过月球,短暂地遮住太阳光并使月球变暗,从而形成月食。
12.从地球上看,当月球从太阳正前方经过,形成日食。
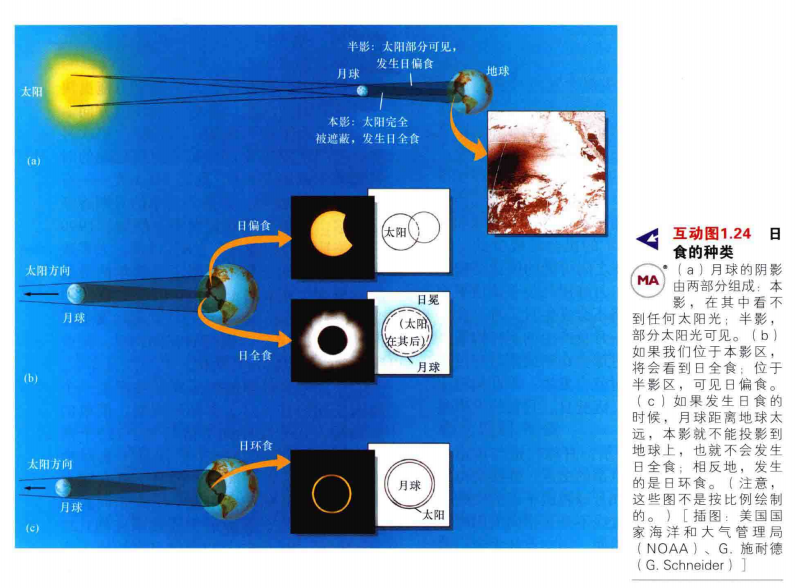
13.当地球,月球,太阳三者完美对齐时候,由于太阳光几乎被完全遮住了,使得大行星和一些恒星在白天也能被看到。上述现象成为日全食。
14.同时我们看到太阳幽灵般的外层大气,即日冕。

15.在本影的阴影中心部分,看到的是日全食;在本影之外的称为半影的阴影部分,看到的是日偏食。
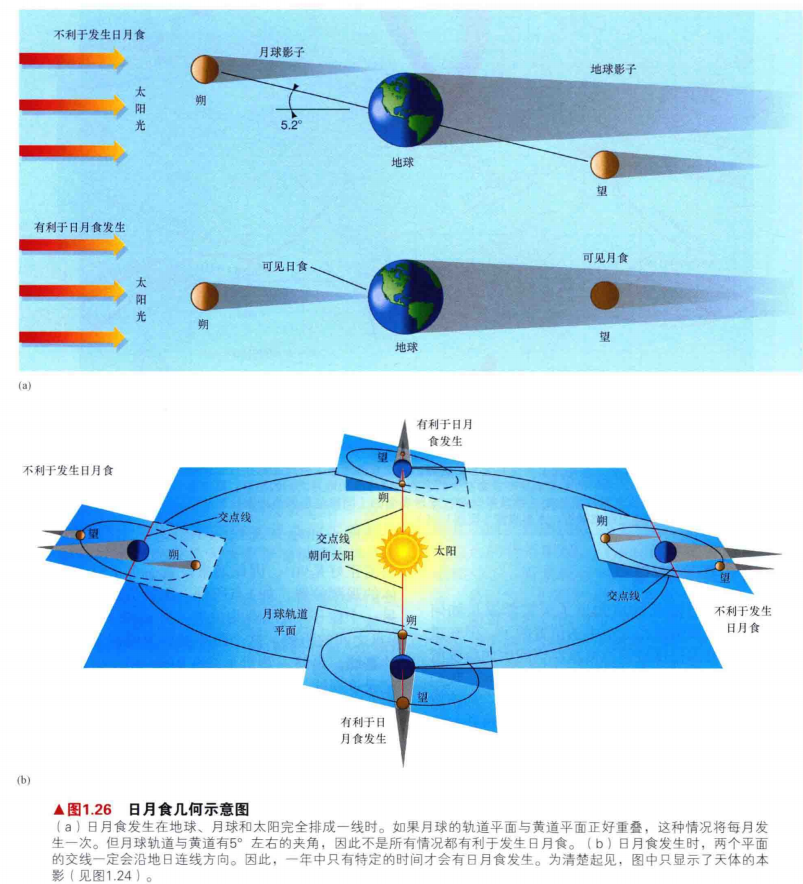
16.月球的轨道与黄道之间存在微小的夹角(角度为5.2°),因此在朔(或望)时,月球恰巧穿过黄道平面(即地球,月球和太阳完美地排成一条线)的机会是极少的。
17.如下图所示,月球轨道与黄道平面的两个交点被称为轨道的交点。连接交点的直线,亦称地球轨道和月球轨道平面的交线,被称为交点线。当交点线不是正指向太阳时,情况不利于发生食。然而,当交点线大致沿着地日连线方向时,食是有可能发生的。这两个时期被称为食季。实际上日食比地面的观测者运动得要快。
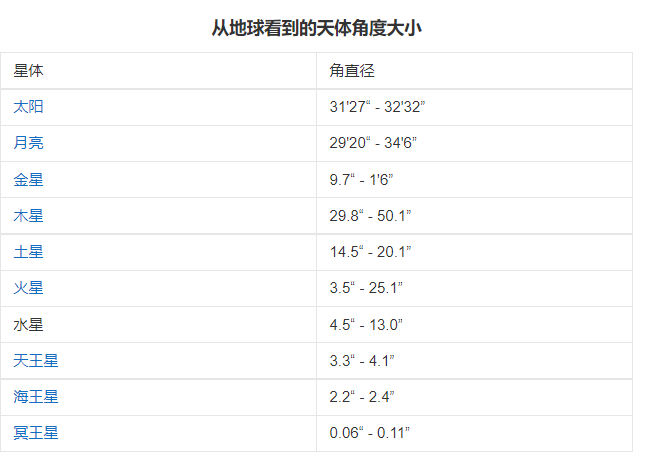
18.事实上,距离之比几乎大小之比一样,因此太阳和月球有着几乎相同得角直径——从地球上看,大约都是0.5°。这样,月球才能几乎完全遮住日面。如果月球更大一些,我们将永远不会看到日环食,而日全食会更为普遍;如果月球更小一些,那我们就只能看到日环食了。
补充知识——角直径
1.角直径(Angular diameter)是以角度做测量单位时,从一个特定位置上观察一个物体所得到得“视直径”。
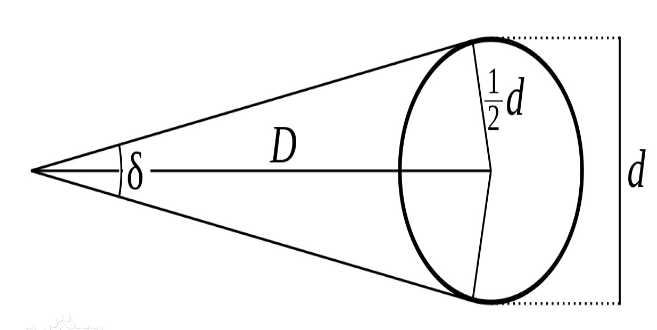
视直径只是被观测得物体在垂直观测者视线方向中心的平面上产生的透视投影的直径。由于它是在观测者的角度下按比例的缩影,因此与物体真实的直径会有所不同。
公式:
19.由于太阳的引力拖曳决定了月球轨道的取向,亦即交点线的方向。因此,交点线指向太阳的位置构型(每次月球都会同样地穿越黄道)前后两次出现地时间间隔并不刚好是1年,而是346.6天——有时这被称为1食年。
20.结合食年和月球地朔望周期会产生一个有趣的长期的日(月)食物循环周期。在此情况下,”同样“的日,月食物就会重现,地球,月球和太阳便会出现相同的相对位置构型。120°的经度变化大约对应于地球自转0.3天,这样的周期被称为沙罗周期。
1.6距离测量
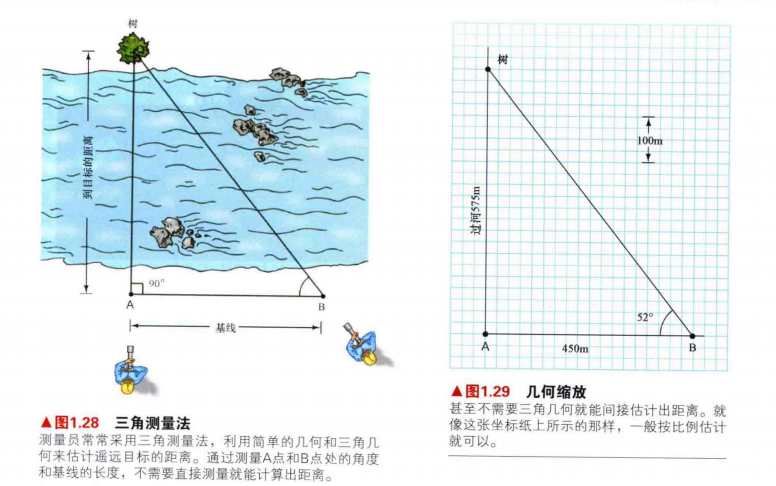
1.三角测量:是借由测量目标点与固定基准线的已知端点的角度,测量目标距离的方法。
2.几何缩放:已知三角测量需要的数据后,在坐标纸上通过比例估计作图,即可估计测量目标点和已知端点之间的长度。
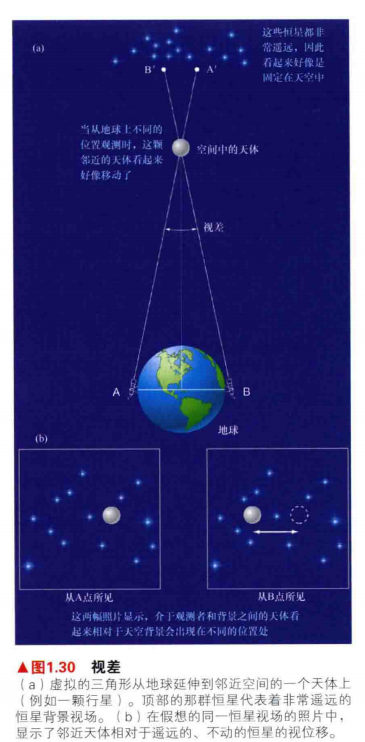
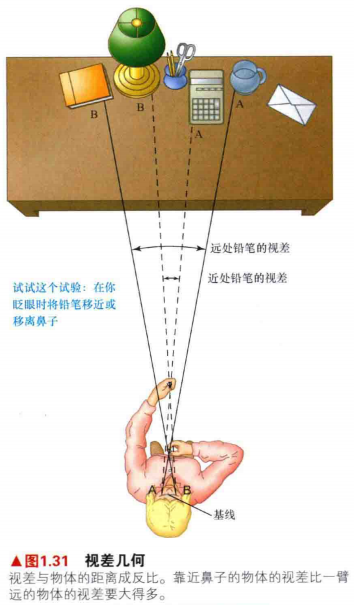
3.随着观测者的位置变化,前景目标相对于背景的视位移被称为视差。物体距离观测者越近,视差越大。换句话说视差的大小与天体成反比。小的视差意味着远的距离,而大的视差则意味着近的距离。
补充知识——利用几何进行距离测量
1.视差:观测者在两个不同位置看同一物体的方向之差,可用于观测者的两个不同位置之间的距离(基线)在天体处的张角表示。
2.弧度(rad):把等于半径长的圆弧所对的圆心角叫做1弧度的角,记作1rad。1rad=206265’。1rad约等于57.3°。
3.行星的视差与其距离相关的推理(示例模型:观测点是地球两端AB,行星是金星):
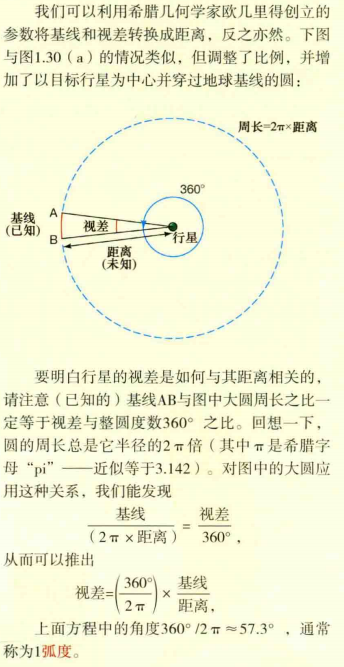
解释1弧度的定义:
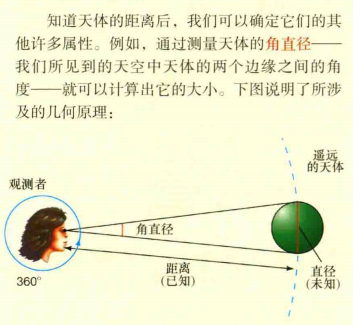
4.知道天体的距离后,我们可以确定它们的其他许多属性。例如,通过测量天体的角直径——我们所见到的天空中天体的两个边缘之间的角度——就可以计算出他的大小。
如下图我们已知了角度(角直径)和距离,而不知道角度(视差)和基线
和上述方程的推理类似,最后得到的方程为:

